mardi, 19 juin 2018
Des « paysages d’attracteurs » pour mieux comprendre les systèmes dynamiques complexes
Une grève étudiante improbable se met en branle au Québec au début de l’année 2012. Comme d’habitude on s’attend à un retour en classe une semaine ou deux après. Mais ça durera des mois pour se transformer en un mouvement social qui viendra à bout du gouvernement Charest.
D’autres luttent depuis des décennies pour une représentation qui reflète mieux la volonté populaire au parlement en demandant un mode de scrutin avec une composante proportionnelle. Et rien ne change.
Voilà deux exemples actualisés de mon coin de pays, mais qui s’apparentent à d’innombrables cas où des systèmes dynamiques complexes semblent bloqués dans un état stable pour soudainement basculer vers un autre état. Un phénomène non seulement observable au niveau social, mais dans de nombreux autres systèmes complexes au niveau des écosystèmes écologiques, de la génétique, du développement cellulaire ou encore, bien entendu, des réseaux de neurones de notre cerveau !
Or il y a un outil très utile pour comprendre ce genre de phénomène qu’on appelle en anglais les « attractor landscapes » (que je traduirais, sans doute maladroitement, par « paysages d’attracteurs », mais je suis preneur s’il y a mieux…). Et pour comprendre cet outil à la fois conceptuel, mathématique et graphique initialement développé en physique, Nicky Case vient de publier cette très bien faite petite « interactive introduction to attractor landscapes ».
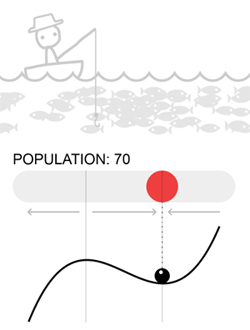
Je me contenterai donc de la résumer en quelques mots… en français. Il part de l’exemple d’un petit lac où l’on peut pêcher les poissons qui s’y trouvent. Ceux-ci se reproduisent et meurent de leur belle mort ou de la pêche. Trois cas se dessinent alors :
1) S’il n’y a pas de pêche, la population va augmenter et avec elle le taux de mortalité par manque de nourriture. Et donc la population va s’autoréguler autour d’une certaine valeur.
2) S’il y a un peu de pêche, la population va se maintenir grâce aux naissances qui vont compenser les individus pêchés.
3) Et s’il y a trop de pêche, la population peut atteindre un seuil minimal critique en deçà duquel elle peut littéralement s’effondrer jusqu’à la disparition des poissons dans ce lac.
Case suppose qu’il pourrait y avoir jusqu’à 100 poissons dans son lac. Mais parce que les ressources y sont limitées, c’est plutôt autour de 70 individus que la population se maintient naturellement s’il n’y a pas de pêche. Si l’on diminue cette population à 60 ou 50 individus en en pêchant 10 ou 20, en peu de temps la population reviendra naturellement à son point d’équilibre de 70 individus. Mais si l’on en pêche plus de 40 et que la population descend à moins de 30 individus, on assiste alors à son effondrement inéluctable jusqu’à 0 individus.
On appelle donc dans cet exemple les valeurs 0 et 70 des attracteurs, tout comme on peut appeler la valeur 30 un « repeller » (un « repoussoir », en français ?) ou encore un « tipping point », un point de non-retour. Car comme on le disait en introduction, tout semblait stable dans ce lac jusqu’à ce moment critique où la population passe sous la barre des 30 individus : tout va alors changer définitivement…
L’animation de Case introduit ensuite l’idée de « paysages » d’attracteurs qui permet de visualiser plus intuitivement le comportement du système en un coup d’œil. Les différentes valeurs du système sont alors intégrées dans une représentation de monts et de vallées où une balle est libre de rouler. Celle-ci va donc naturellement se retrouver dans les vallées, endroit beaucoup plus stable que la cime arrondie des monts. Autrement dit, les monts sont des repoussoirs et les vallées des attracteurs !
Des choses deviennent alors évidentes grâce à ce type de représentation. Ainsi, plus une vallée sera profonde, plus il faudra d’énergie pour s’en échapper. L’attracteur 0 rend par exemple l’effondrement de la population quasi inévitable vu sa grande profondeur.
La largeur d’une vallée dénote pour sa part ce qu’on appelle le « bassin d’attraction », c’est-à-dire l’étendue des valeurs qui seront attirées par l’attracteur situé au point le plus bas de cette vallée. Dans notre exemple, le bassin d’attraction de la valeur 70 s’étend donc de 30 à 100.
Case fait remarquer qu’il n’y a qu’un seul paramètre qui varie dans son exemple, soit la population. C’est pour ça qu’on peut représenter son paysage d’attracteurs sur un graphique en deux dimensions. Mais si l’on avait deux paramètres, il faudrait une représentation 3D comme celle-ci-dessous.
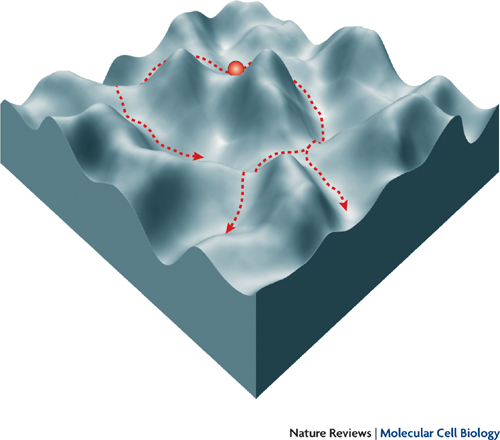
Rien ne nous empêche d’avoir plus de paramètres encore, avec toujours une dimension de plus nécessaire pour les représenter (ce qui se fait moins facilement au-delà de trois dimensions…). Et dans les systèmes complexes avec énormément de paramètres, on tend vers les fameux « attracteurs étranges » des phénomènes chaotiques.
La beauté de la chose avec les paysages d’attracteurs, c’est donc qu’ils permettent aussi de modéliser différentes situations d’un même contexte. Dans notre exemple de lac par exemple, qu’arriverait-il si l’on augmentait la capacité du lac à produire plus de plantes aquatiques pour nourrir les poissons ? Ou si l’on introduisait une population de prédateurs, comme le brochet ou le héron, en plus de la pêche humaine ? Ce n’est plus alors la balle dans le relief du paysage d’attracteurs qui va bouger, mais le relief du paysage d’attracteurs lui-même qui va être modifié pour correspondre à la nouvelle situation !
Par conséquent, lorsqu’une situation (sociale, politique…) nous semble désespérément bloquée, l’idée de chercher à la comprendre en termes de d’attracteurs, de profondeur des vallées de ces attracteurs, de largeur du bassin d’attraction ou de possibilités de modifier carrément le paysage des attracteurs est peut-être une bonne approche pour y voir plus clair. Après tout, il y a tant d’exemples, quand on y pense, où rien de ne semble bouger et où tout d’un coup tout peut changer…
* * *
Je m’aperçois que je n’ai pas donné d’exemples en neurobiologie où pourtant les paysages d’attracteurs permettent de comprendre bien des choses. Ce sera donc pour le prochain billet qui sera non pas la semaine prochaine mais dans deux semaines. Je serai en effet la semaine prochaine sur les routes du Québec pour une première petite escapade à vélo, histoire de faire du bien à mon cerveau et à mon système immunitaire. J’espère que vous pourrez en faire autant cet été !
Non classé | Comments Closed
