lundi, 17 février 2020
Différents modèles non linéraires pour modéliser l’activité dynamique cérébrale
C’est donc cette semaine que reprend le cours « Notre cerveau à tous les niveaux », donné en collaboration avec l’UPop Montréal. Comme je le rappelais la semaine dernière, il s’agit de la suite de cette série de 10 séances dont 5 ont été données cet automne au café Les Oubliettes. Comment se poursuivra cette aventure où chaque séance « en rajoute une couche » en terme de complexité ? La séance de ce mercredi 19 février, la 6e de la série, aborde la question des patterns d’activité électrique rythmique qui émergent des réseaux cérébraux de milliards de neurones dont on avait parlé à la 5e séance.
Car jusqu’ici dans ce cours, on a regardé des cartes cérébrales qui nous indiquent comment se déploient nos voies nerveuses, donc les chemins possibles pour les influx nerveux. Mais, pour employer une métaphore routière, ces cartes ne nous disent rien sur l’intense trafic du matin et du soir versus le calme du milieu de journée, la direction prédominante du trafic à ces différents moments, ses cycles plus lents comme la tranquillité des vacances d’été et de Noël versus la plus grande activité le reste de l’année, etc. Et ce sera la même chose pour le cerveau qui possède toutes sortes de rythmes à différentes échelles de temps et selon les régions observées.
Autrement dit, nos circuits nerveux forment des réseaux anatomiques, mais dans lesquels se propage de l’activité nerveuse qui va former des systèmes dynamiques non linéaire. Qu’est-ce que tout cela veut dire ? On parle donc d’abord d’un système qui est dynamique, c’est-à-dire un système dont les variables (ou la forme) varient dans le temps. Mais on qualifie aussi ce système de non linéaire. Pourquoi ?
Depuis la physique de Newton et même avant, on peut expliquer beaucoup de phénomènes en terme de causalité linéaire. Une cause produit un effet, qui peut à son tour produire un autre effet, etc. Sauf que dans un système complexe comme le cerveau, les interactions et les connexions se font dans toutes les directions. Elles forment souvent des boucles qui reviennent sur elles-mêmes. C’est ce genre d’interactions, extrêmement nombreuses et souvent réciproques, qui donnent lieu à des relations causales non linéaires. Ou, pour le dire comme le philosophe Michael Anderson :
“The brain is decidedly not a primarily feed-forward system.”
Pour comprendre parfaitement de tels systèmes dynamiques non linéaires, il faudrait connaître à tout moment l’état et le taux de variation de chaque variable pertinente. Mais dans un système dynamique complexe comme le moindre neurone, c’est impossible d’avoir accès à l’état de ses innombrables éléments comme l’ouverture ou non de ses canaux membranaires, le niveau d’activité de tel ou tel enzyme, etc. Une description complète des variations temporelles d’un tel système est donc impossible. Et donc il faut faire des simulations avec des modèles dynamiques non linéaires. Mais des modèles de comportements dynamiques dans un système, il en existe de nombreux types. Lesquels sont les plus pertinents quand on parle de l’activité nerveuse dans le cerveau ?
Je vais en explorer quelques-uns durant la séance de mercredi, me contentant de les évoquer brièvement à partir d’un billet que j’avais écrit en juin 2018 et qui s’intitulait Des « paysages d’attracteurs » pour mieux comprendre les systèmes dynamiques complexes. Ce billet expliquait le concept d’« attractor landscapes » (que l’on pourrait traduire par « paysages d’attracteurs ») à l’aide de l’exemple d’un petit lac où l’on peut pêcher les poissons qui s’y trouvent. Ceux-ci se reproduisent et meurent de leur belle mort ou de la pêche. Il s’agit donc un système dynamique, et dans notre exemple :
« …il pourrait y avoir jusqu’à 100 poissons dans [le] lac. Mais parce que les ressources y sont limitées, c’est plutôt autour de 70 individus que la population se maintient naturellement s’il n’y a pas de pêche. Si l’on diminue cette population à 60 ou 50 individus en en pêchant 10 ou 20, en peu de temps la population reviendra naturellement à son point d’équilibre de 70 individus. Mais si l’on en pêche plus de 40 et que la population descend à moins de 30 individus, on assiste alors à son effondrement inéluctable jusqu’à 0 individus.
On appelle donc dans cet exemple les valeurs 0 et 70 des attracteurs, tout comme on peut appeler la valeur 30 un « repeller » (un « repoussoir », en français ?) ou encore un « tipping point », un point de non-retour. »
Et donc cette idée de « paysages » d’attracteurs va permettre de visualiser plus intuitivement le comportement d’un tel système complexe.
« Les différentes valeurs du système sont alors intégrées dans une représentation de monts et de vallées où une balle est libre de rouler. Celle-ci va donc naturellement se retrouver dans les vallées, endroit beaucoup plus stable que la cime arrondie des monts. Autrement dit, les monts sont des repoussoirs et les vallées des attracteurs ! »
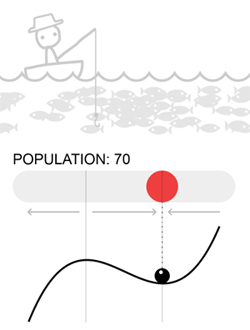Dans notre exemple, il n’y avait qu’un seul paramètre qui variait (la population de poisson) ce qui permettait de représenter son paysage d’attracteurs sur un graphique en deux dimensions comme celui contre.
Il y a plusieurs types d’attracteurs possibles et celui-ci entre dans la catégorie des attracteurs qui sont de simple point (« point attractor state », en anglais). Autrement dit, il peut y avoir des variations dans les conditions, mais si celle-ci ne sont pas trop grandes, le système aura tendance à revenir à une certaine valeur qui est cet attracteur point. Ainsi, une population de neurones peut, en présence d’un stimulus, adopter un rythme différent, mais stable, d’émission de ses influx nerveux. Cette nouvelle fréquence de décharge peut alors être considérée comme un attracteur ponctuel dans cette nouvelle condition.
Revenons à nos paysages d’attracteurs. Si l’on avait maintenant non pas un mais deux paramètres, il faudrait une représentation 3D comme ceci :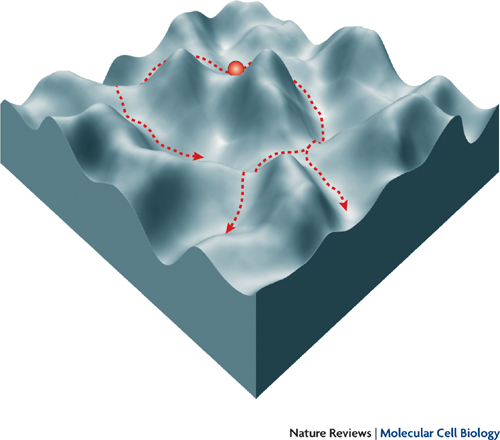 
Notez qu’un système complexe peut avoir bien plus de paramètres encore, ce qui n’empêche pas de les modéliser avec toujours une dimension de plus nécessaire pour les représenter (ce qui se visualise cependant moins facilement au-delà de trois dimensions…).
Un système peut aussi posséder plusieurs attracteurs ponctuels. L’état d’activité d’un tel circuit neuronal à un instant donné – c’est-à-dire l’attracteur particulier dans lequel il réside – dépendra de l’activité antérieure dans le système. J’en avais donné un exemple dans un second billet publié en juillet 2018. J’y rappelais que ce sont souvent des paysages d’attracteurs qui sont utilisés pour modéliser ce qu’on appelle un engramme mnésique, autrement dit la trace neuronal d’un souvenir dans notre cerveau. Celle-ci correspond à certaines assemblées de neurones sélectionnées, c’est-à-dire « habituées de travailler ensemble », si vous voulez.
Dans la jungle immense de neurones que constitue notre cerveau, il y aurait donc certains réseaux sélectionnés par l’apprentissage où l’activité nerveuse aurait tendance à se produire plus souvent, à se maintenir plus longtemps, etc. Un peu comme lorsqu’une feuille d’arbre tombée dans un torrent reste prise dans un tourbillon derrière une roche, et puis tout d’un coup, profitant d’une fluctuation de l’eau un peu plus importante, s’en échappe pour se reprendre dans le tourbillon d’à côté. On voit donc aisément l’analogie avec un paysage aux multiples attracteurs. Quand on apprend quelque chose, on modifie nos connexions synaptiques et donc, à la longue, nos paysages d’attracteurs. Résultat : nos comportements tendront à être différents après l’apprentissage parce notre activité nerveuse se stabilisera ailleurs, dans de nouveaux attracteurs.
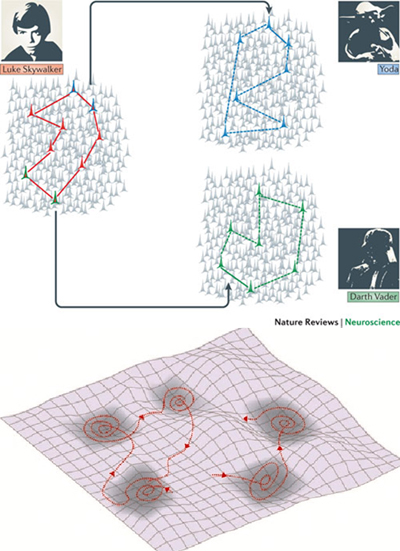L’idée de ce qu’on appelle en anglais « pattern completion » peut aussi être comprise à travers ce type de paysage aux multiples attracteurs. Certains neurones étant communs par exemple au réseau codant pour l’image mentale de Luke Skywalker, le Yoda et Darth Vader (parce que mémorisés dans le même contexte du film Star Wars), penser à l’un nous fait souvent penser irrémédiablement à l’autre, sans doute par un phénomène « d’embrasement » de l’activité de l’assemblée neuronale voisine par l’entremise de leurs neurones communs. Ou, pour parler en termes de paysage d’attracteurs, de passage ou de « glissement » d’une vallée à une vallée voisine.
Un autre exemple serait ces figures dites « bistables » où notre perception bascule constamment entre deux images différentes évoquées par le même stimulus ambigu comme le cube de Necker. Les modèles expliquant ce phénomène suggère un circuit nerveux possédant deux attracteurs avec différents facteurs plus ou moins connus encore qui détermineraient la bifurcation d’un attracteur à l’autre.
Un autre cas de système dynamique est celui où il génère des oscillations. Des états initiaux variés dans un tel système vont converger vers des fluctuations cycliques ayant une fréquence donnée. Ce type d’attracteur cyclique est extrêmement répandu dans le cerveau et beaucoup de recherches tentent d’élucider le rôle de ces rythmes cérébraux. On en parlera amplement durant la séance de mercredi, notamment sur les sources de ces oscillations d’activité nerveuse qui peuvent être intrinsèques aux neurones eux-mêmes ou provenir de la connectivité des circuits. J’ai résumé cette partie important du cours dans ce billet sur un cours que j’avais donné à l’UQAM et dans cet autre donné à l’UTA. C’est pourquoi je ne les détaillerai pas davantage ici.
Je terminerai en mentionnant une dernière famille de modèles de systèmes dynamiques non linéaires, celle des systèmes chaotiques. Dans de tels modèles, l’état du système peut suivre un itinéraire imprévisible entre différents états ou encore osciller entre certains états mais de façon irrégulière et imprévisible. D’où leur nom « d’attracteurs étranges ». Et surtout, de toutes petites variations dans les conditions de tels systèmes peuvent amener de très grands changements dans le comportement du système.
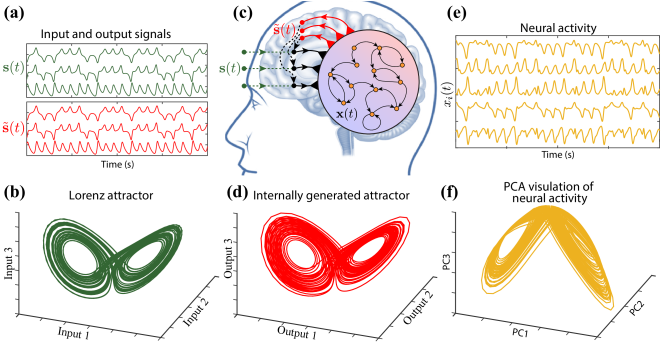
Un exemple en neurobiologie de ceci pourrait être les travaux pionniers de Walter J. Freeman qui tentait de comprendre comment le cerveau donne du sens à un stimulus. Pour ce faire, Freeman entraînait des lapins à répondre à des odeurs pendant qu’il enregistrait les patterns d’activité électrique dans le bulbe olfactif. Il a ainsi découvert qu’en l’absence d’une odeur familière, le système olfactif du lapin se comporte selon un attracteur chaotique. Mais si l’on présente une odeur familière à l’animal, la dynamique du système devient plus ordonnée, un peu comme un attracteur cyclique. Un autre exemple plus récent (et plus complexe) se retrouve dans l’article de 2018 : « A Parsimonious Dynamical Model for Structural Learning in the Human Brain » (dont l’image illustrant ce billet est tirée).
Mais il faut garder à l’esprit qu’un même système avec des milliers de neurones peut se comporter selon différents modèles dynamique dépendamment des assemblées de neurones qui sont les plus activées à un moment donné. C’est de tout cela (et bien d’autres choses encore !) dont nous discuterons mercredi.
Non classé | Comments Closed
